Opa, tem dois conceitos que é bom conhecer antes de implementar qualquer algoritmo pathfinding: um
Grafo e uma
Fila de prioridade.
Quanto ao algoritmo em si, se você só quer encontrar um caminho (qualquer que seja) o que você precisa é basicamente 1. uma função de V -> V[] que dado um vértice te dá todos os vértices ligados a ele (i.e. seus "vizinhos") e 2. uma forma de testar todos os caminhos possíveis.
No caso do RPG Maker, o grafo é simplificado porque é uma
grade quadriculada, então determinar os vizinhos é bem simples (só somar as coordenadas!). Então, basicamente, nosso conjunto de vértices vai ser
[0...m) x [0...n), onde m e n são a largura e altura do mapa (i.e., todos os pares (x, y) onde 0 <= x < m e 0 <= y < n), e nosso conjunto de arestas vai ser
A = { (p, q) | p, q ∈ V e d1(p, q) = 1 } (
d1 =
distância de manhattan, que é um jeito bonito de dizer "quantos quadradinhos de distância"). Isso assumindo só movimento em 4 direções, movimento diagonal fica como exercício haha
(
Status: temos
V = [0...m) x [0...n) e
A = { (p, q) | p, q ∈ V e d1(p, q) = 1 })
Agora vamos supor um mapa assim:
Temos:
V = [1...6] x [1...9],
S = (1, 5),
E = (6, 1).
Agora, o que significa agora achar um caminho de S para E? Um caminho é uma sequência finita de vértices onde:
(n = tamanho da sequência)
Ou seja, o primeiro elemento da sequência é S, o último é E, e de cada elemento para o próximo existe uma aresta. Dado que aceitamos essa definição, qualquer sequência que encontrarmos e que satisfaça essa condição resolve nosso problema.
Tem um detalhe nesse mapa, porém, que também existe no RPG Maker e que nossa definição do grafo ainda não cobre: existem posições no mapa que não são atravessáveis, e essas posições não podem fazer parte de um caminho.
Tem um jeito fácil de resolver isso: sumir com os vértices das posições que não são atravessáveis. Pra isso, vou invocar uma função qualquer
pass(v) que me diz se um tile é passável (no RPG Maker, essa seria a
Game_Map#isPassable). Com ela, os novos vértices ficam:
V' = { p ∈ V | pass(p) } (ou seja, os mesmos vértices de antes, desde que sejam atravessáveis).
Se fosse para desenhar no mapa os vértices e arestas do grafo agora, teríamos a seguinte figura:
Com isso, temos a base pra fazer um algoritmo simples de busca de caminho. O mais simples seria assim (pseudocódigo):
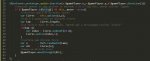
Código:
def find_path(vertices, edges, start, end, visited = {}, path = []):
if start = end:
return path + [end]
else:
visited' := visited ∪ { start }
path' := path + [start]
for neighbor in { v | v ∉ visited && (start, v) ∈ edges }:
path'' := find_path(vertices, edges, neighbor, end, visited', path')
if path'' != ∅:
return path''
return ∅
Explicando: é uma função recursiva, que varia o ponto de início e vai construindo o caminho em uma variável passada por argumento.
Como toda boa função recursiva, temos um caso base:
Código:
if start == end:
return path + [end]
Nesse caso, a base é
start == end, que significa um caminho de um ponto para ele mesmo. Nesse caso, claro que o caminho tem só um ponto, que é o próprio fim (e começo, eles são iguais).
Além do caso base, claro, temos um passo recursivo:
Código:
visited' := visited ∪ { start }
path' := path + [start]
for neighbor in { v | v ∉ visited && (start, v) ∈ edges }:
path'' := find_path(vertices, edges, neighbor, end, visited', path')
if path'' != ∅:
return path''
return ∅
Aqui a gente mantém um conjunto de vértices já visitados (pra não entrar em loop: como as arestas são bidirecionais, se não fizermos isso o próximo vizinho vai chamar a função pra esse mesmo ponto de novo) e colocamos o vértice que visitamos no caminho que estamos construindo. Daí, a recursão acontece: o caminho atual é o caminho que achamos até agora, mais qualquer que seja o caminho que vamos achar a partir do nosso vizinho.
Tem um caso especial também que é quando não é possível achar nenhum caminho, porque não tem vizinhos pelos quais dá pra achar um caminho. Nesse caso, a gente retorna ∅ (vazio, nulo, nenhum caminho).
Coisas a se manter em mente: esse algoritmo é MUITO INEFICIENTE. O tempo de execução dele é exponencial de acordo com o número de arestas. Ele também não garante que vai achar o menor caminho, o que geralmente é desejável.
Por que eu expliquei ele? Primeiro, porque todo mundo sempre lembra do Dijkstra e A* quando a gente pensa em buscar caminhos, mas esse algoritmo tem um nome também:
Backtracking (uma variação dele, pelo menos). É um algoritmo bem essencial e mais geral que Dijkstra ou A*, que você pode usar pra outras coisas como por exemplo
resolver sudoku.
Segundo, porque é um algoritmo mais simples de entender que os outros mais especializados, e a base é parecida (a maior diferença vai ser que ao invés de usar a pilha, fazendo recursão, você vai usar uma fila ou fila de prioridade, e botar uma heurística no caso do A*).
Se quiser uma implementação pronta de A* no RPG Maker, tem o meu gist pro VX Ace:
Script de pathfinding (menor caminho) para RPG Maker VX Ace. A maior diferença pro MZ é que é em Ruby, em termos de API teve muito pouca mudança desde o VX Ace, pelo menos no que tange a parte que o script usa.