Conhecimento necessário : médio
[box class=windowbg]Soma-Zero(Zero-Sum)
[/box][box class=windowbg2]
Para nossa terceira aulinha já chegamos em um algoritmo bem interessante, Minimax. Antes de falar em si do minimax, acho importante dizer aonde ele é aplicável, e sua aplicação são para jogos "Soma-Zero". Soma-Zero nada mais é do que jogos que a quantidade partidas vencidas por você, é exatamente a quantidade de partidas que seus oponentes perderam e se você está ganhando alguém está perdendo proporcionalmente, ou seja jogo-da-velha, jogos de carta, xadrez, damas etc. Para esse algoritmo é bom entender que ele é aplicável para esses tipos de jogos.
[box class=windowbg]
Minimax[size]
[/box]Antes de falar do minimax, para dar aquele incentivo extra, saiba que foi esse algoritmo que derrotou Gary Kasparov, mestre do xadrez, em 1997, algoritmo apelidade de "Deep Blue", ou seja agora estão prestes a aprender o algoritmo que surpreendeu o mundo. A ideia do Minimax ou Maximin é bem simples, em um jogo de turnos eu devo maximizar a chance de vencer quando estou no meu turno e quando estiver no turno do oponente devo minimizar a chance de vitória. Para jogos de turnos finitos, como o jogo-da-velha, é possível realizar a IA praticamente perfeita por ter mapeado todas as jogadas possíveis.
Como funciona o algoritmo? Primeiro você tem que ter os pesos nas decisões vide a primeira aula. Vamos pegar o jogo-da-velha como exemplo, como ele só tem jogadas do tipo vitória, neutro (sem decisão do vencedor ainda) e derrota, vamos considerar vitória = +1 derrota = -1 e o empate = 0, o neutro para o jogo-da-velha consideraremos sem pontuação. Os neutros serão pontuados de acordo com a decisão de vitória e derrota, segue abaixo o exemplo:

Primeiro montamos a árvore, sempre que o resultado não é deterministico adicionamos os filhos de acordo com as possibilidades, quando ele é deterministico (empate, vitória ou derrota), adicionamos a nota para aquele nó. Feito isso fazemos de cima para baixo, max-min-max-min-max.... até a herança completa da árvore. Por último de baixo para cima, se for max, passamos o valor mais alto dos filhos para cima, se for mínimo, passamos o valor mínimo para cima. Isso até alcançar a jogada 1, que é a jogada atual da máquina, como podem ver pela imagem o resultado já foi definido, a máquina sabe que vai conseguir o +1 que seria a vitória dela.
Qual é a lógica de tudo isso? Bom a ideia é que sempre que tem os nós de "Minimo", ele escolhe como os caminhos que ele deve evitar caso o oponente vença, sempre que tem os caminhos como "Máximo", ele vai optar pelos caminhos que lhe dão a vitória.
[box class=windowbg]
[size=12pt]Alpha-Beta Pruning[size]
[/box][box class=windowbg2]
Estão craques no Minimax já? Que tal otimizarmos o código? O que acontece é que o Minimax varre todas as possibilidades possíveis, no caso do jogo-da-velha que usamos como exemplo (3^9 = 196839), muito não? Agora imagina para um jogo de xadrez ou damas. Para que ele não faça a varredura completa e melhore a performance do nosso algoritmo, usamos uma técnica chamada "poda alfa-beta". Como ele funciona? Lembra como eu passei os valores de baixo para cima para completar? Pois a poda alfa-beta vem de cima para baixo para tentar cortar cálculos desnecessários. Vamos na prática como isso funciona.

Quais os valores possíveis para o Nó A? no caso seria isso -infinito ou +infinito, correto? Vamos chamar os valores de alfa e beta, alfa é o calculado e beta é o que vamos calcular.
[*] no caso o A seria Max(-inf, +inf) no momento.
[*] Nó B, Min(+inf, -inf) a troca dos sinais é porque o beta sempre tem que iniciar como o valor a ser calculado, porque ele é a variável.
[*] Nó D, é máximo, como o valor é max, ele deve ser colocado no valor beta (+infinito), logo no D fazemos para o primeiro valor 1 no lugar de beta. Ficando (-inf, 1).
[*] Nó D para o segundo valor, fazemos sempre o questionamento, o valor que temos é maior que o beta do nó acima?(+inf), 1 >= +inf? Não então verificamos o 3. 3 é maior que 1? Sim, logo para o nó D temos Min(-inf, 3). Complicado? Em breve irá clarear tudo
[*] Passamos para o Nó E, temos Min(3, +inf) , porque o 3? O 3 foi o valor encontrado pelo outro nó, logo ele passa a ter o valor de alfa porque alfa seria o valor mínimo possível e sabemos que o valor mínimo possível de lá é 3. o primeiro valor do nó E é 5, então Min(3, 5), não precisamos mais verificar os outros valores, já o valor escolhido sempre será o 3.
[*] Nó B, Min(3, 5) nó B fica com valor 3.
[*] Nó A, Max(3, +inf), ainda não deterministico, temos que ir para o nó C.
[*] Nó C, Min(3, -inf) beta ainda desconhecido, então descemos na árvore
[*] Nó F, Max(3, +inf), temos que validar o beta, primeiro o beta é 1, 1 >= +inf? não então temos que analizar o outro valor do nó F.
[*] 1 >= 2? não então o 2 é o valor de beta, que então é passado para o nó F.
[*] Nó C, Min(2, +inf), Temos que ir para o nó G.
[*] Nó G, Max(2, 7), logo escolhemos o 7 como beta, não é necessário validar o próximo valor.
Resumindo tudo, esse é um modo que a máquina enxerga e como passamos a lógica para ela, a ideia nada mais é do que , tenho um valor mínimo já, esse valor mínimo já é menor que toda a sequencia de nós a direita? Sim? Então podemos ignorar ela inteira e passar esse valor para o nó acima. O mesmo sendo feito para o máximo.
Ainda um pouco complicado certo? Vamos a mais um exemplo:
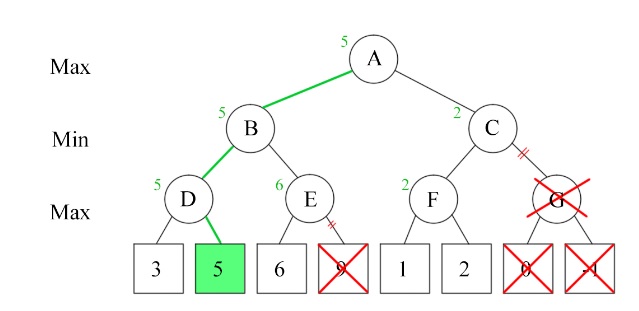
Agora de um modo mais dinamico:
Nó A Max(-inf, +inf),
Nó B não determinado Min(+inf, -inf),
Nó D, Max(3, +inf), limite acima +inf, continua, no caso 5 é maior que 3, passa 5 para o D.
Nó B, Min(5, -inf), valida o nó E
Nó E, Max(5, +inf), passa o 6, Nó B passa a ser Min (5, 6 até +inf), logo beta sempre será maior que alpha, então não precisamos validar os seguintes.
Sobe os valores, Nó A, Max(5, +inf), continuamos a descer na árvore
Nó C Min(5, -inf).
Nó F Max(5, +inf), Nó F passa a ser Max (5, 1 até +inf), não deterministico, olhamos para o outro valor,
Nó F o alfa passa a ser Max(5, 2), passamos o valor 2, mas com a comparação a alfa ele é abaixo de 5. logo não há porque calcular o nó G, o valor dele sempre será.
Nó G, Min (2, +inf), o que dará sempre 2.
[/box]
[box class=windowbg]
[size=12pt]Finalizando
[/box][box class=windowbg2]
Esse foi mais complicado, espero que eu tenha conseguido explicar tudo direito, caso tenha alguma dúvida só avisar aqui!
[/box]

